Kk absolutwert und argument, Kk konjugiert komplexe zahlen – Casio FX-9860G Benutzerhandbuch
Seite 109
20050401
2-6-3
Rechnen mit komplexen Zahlen
k
k
k
k
k Absolutwert und Argument
[OPTN]-[CPLX]-[Abs]/[Arg]
Der Rechner interpretiert jede komplexe Zahl in der Form Z =
a
+
bi
als Punkt oder Koordi-
natenpaar (
a
,
b
) in der der Gauß'schen Zahlenebene und berechnet den Absolutwert Z
und das Argument (arg Z) mit Hilfe des Koordinatenpaares (
a
,
b
).
○ ○ ○ ○ ○
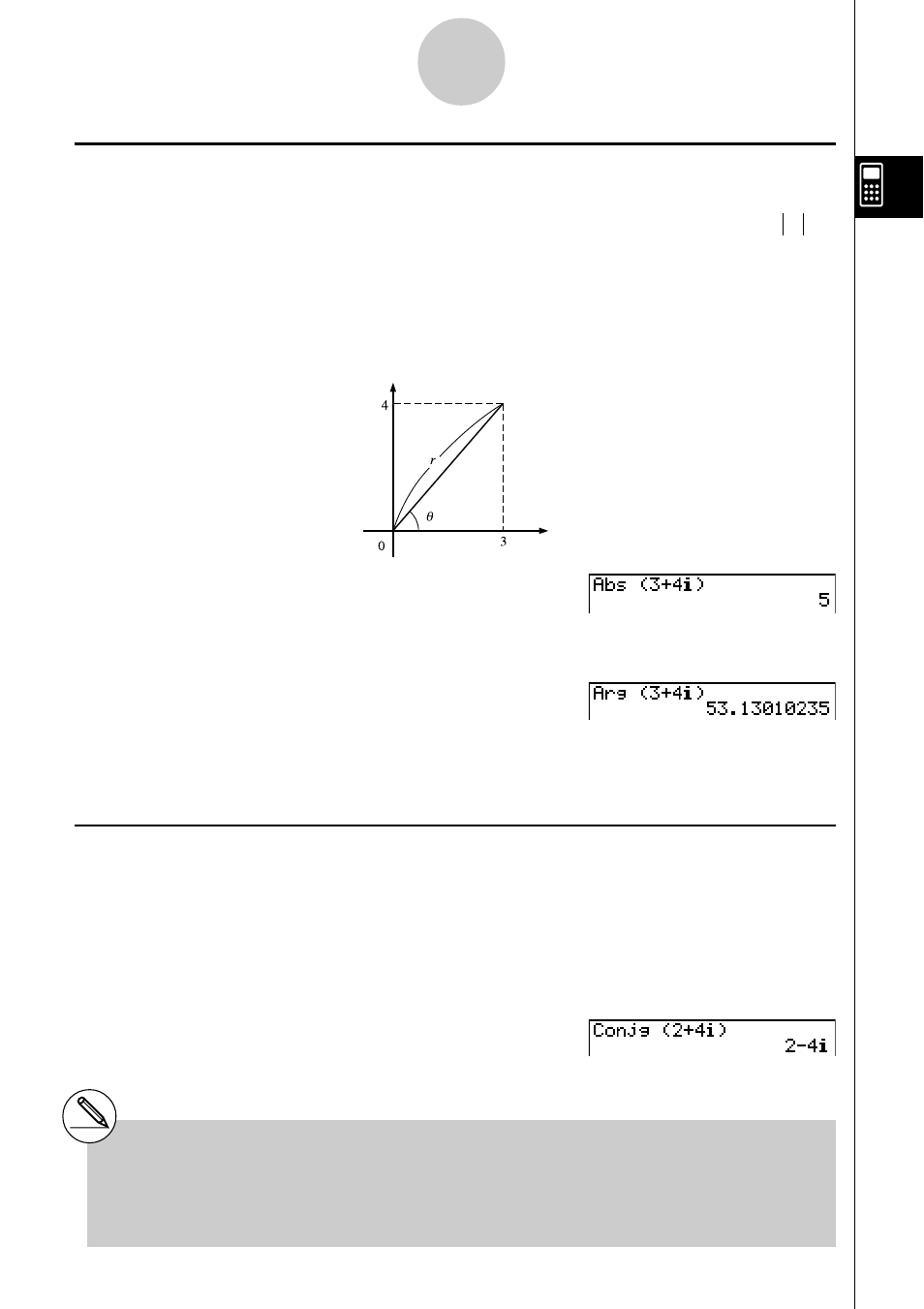
Beispiel
Zu berechnen sind der Absolutwert (
r
) und das Argument (
θ) für die
komplexe Zahl 3 + 4
i
, wobei der Winkelmodus auf Altgrad eingestellt
werden soll.
AK3(CPLX)2(Abs)
(d+e
1(
i
))w
(Berechnung des Absolutwertes (Betrages))
AK3(CPLX)3(Arg)
(d+e
1(
i
))w
(Berechnung des Arguments (Winkels))
k
k
k
k
k Konjugiert komplexe Zahlen
[OPTN]-[CPLX]-[Conj]
Eine komplexe Zahl der Form
a + bi
wird in die konjugiert komplexe Zahl der Form
a – bi
umgeformt.
○ ○ ○ ○ ○
Beispiel
Zu berechnen ist die konjugiert komplexe Zahl zur komplexen Zahl
2 + 4
i
AK3(CPLX)4(Conj)
(c+e
1(
i
))w
# Das Ergebnis der Argumentberechnung
unterscheidet sich in Abhängigkeit vom
aktuell eingestellten Winkelmodus (Altgrad,
Bogenmaß, Neugrad).
Imaginäre Achse
Reelle Achse