Casio fx-9860G Slim Benutzerhandbuch
Seite 353
20070201
u Verteilungsfunktion einer N(
μ
,
σ
2
) - Verteilung
In diesem Untermenü kann mithilfe der Verteilungsfunktion einer Normalverteilung un-
kompliziert eine Intervallwahrscheinlichkeit der Form
p
=
P(
X
P
[a, b]
)
=
P(
a
≤
X
≤
b
)
für eine
Normalverteilung berechnet werden.
a
: Untere Intervallgrenze
b
: Obere Intervallgrenze
Führen Sie die folgende Tastenbedienung im STAT-Eingangsmenü (Listeneditor) aus.
5(DIST) ...
Wahrscheinlichkeitsverteilung
1(NORM) ... Normalverteilung
2(Ncd) ...
Verteilungsfunktion
Folgende Positionen erscheinen im Eingabefenster zur Festlegung der Parameter (Vorgabe-
werte, Einstellungen). Nachfolgend wird die Bedeutung der einzelnen Positionen beschrieben.
Lower .......................... Untere Intervallgrenze
a
Upper .......................... Obere Intervallgrenze
b
σ ................................. Standardabweichung der N
(
μ
,
σ
2
)
-Verteilung (
σ
> 0)
μ ................................. Mittelwert der N
(
μ
,
σ
2
)
-Verteilung
Save Res .................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-
nisse (Keine [None] oder Liste 1 bis 26)
Execute ....................... Führt die Berechnung aus
Nachdem Sie alle Parameter (Vorgabewerte) eingestellt haben, verwenden Sie die
c-Taste zur
Hervorhebung von „Execute“, und drücken danach die nachfolgend dargestellte Funktionstaste,
um die Berechnung auszuführen.
•
1(CALC) ... Führt die Berechnung der Intervallwahrscheinlichkeit
p
aus.
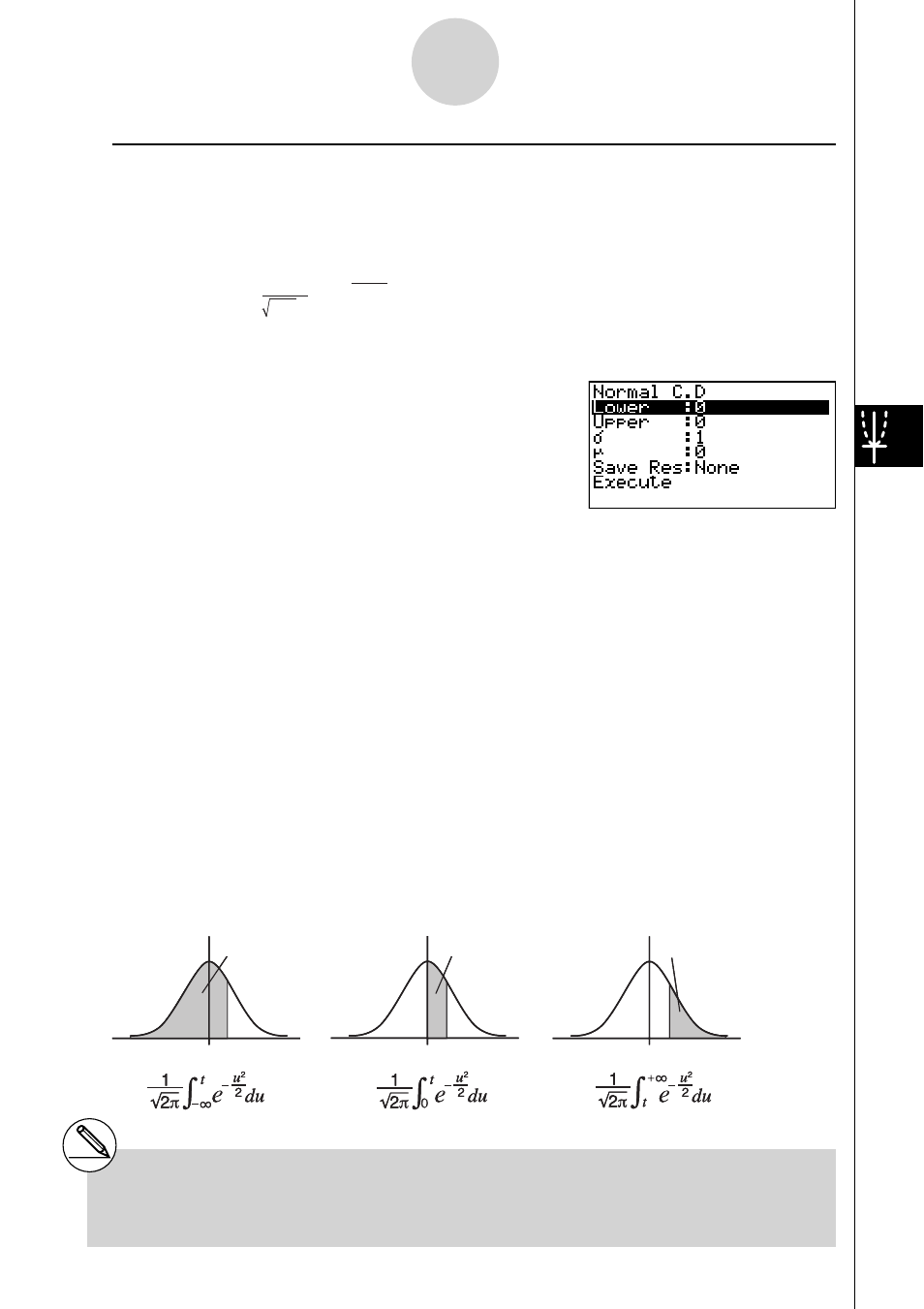
Hinweis: Weitere Intervallwahrscheinlichkeiten können über die Funktionen P(t), Q(t) und
R(t) im RUN•MAT-Menü (Untermenü [OPTN], [PROB], [P( ] oder [Q( ] oder [R( ] )
berechnet werden, vgl. S. 6-4-7 bis 6-4-10:
πσ
2
p
=
1
e
–
dx
2
2
σ
(x –
μ
)
2
μ
a
b
∫
πσ
2
p
=
1
e
–
dx
2
2
σ
(x –
μ
)
2
μ
a
b
∫
P (
t
)
Q (
t
)
R (
t
)
t
t
t
0
0
0
P (
t
)
Q (
t
)
R (
t
)
t
t
t
0
0
0
# Für die Intervallwahrscheinlichkeit einer
Normalverteilung kann im STAT-Menü keine
Wahrscheinlichkeits-Grafi k gezeichnet werden.
# Im GRAPH-Menü kann die N(0,1) -Vertei-
6-7-4
Wahrscheinlichkeitsverteilungen
lungsfunktion als Y=P(X) gezeichnet werden.
Intervallwahrscheinlichkeiten können dort als
Flächenanteil unter der Gaußschen Glockenkurve
schraffi ert werden (Ungleichungsgrafi k nutzen).