Winkelfunktionen (engl. trigonometry), 3 winkelfunktionen (trigonometrie), Bc a α – HEIDENHAIN TNC 407 (280 580) User Manual Benutzerhandbuch
Seite 193
TNC 425/TNC 415 B/TNC 407
7-8
7
Programmieren mit Q-Parametern
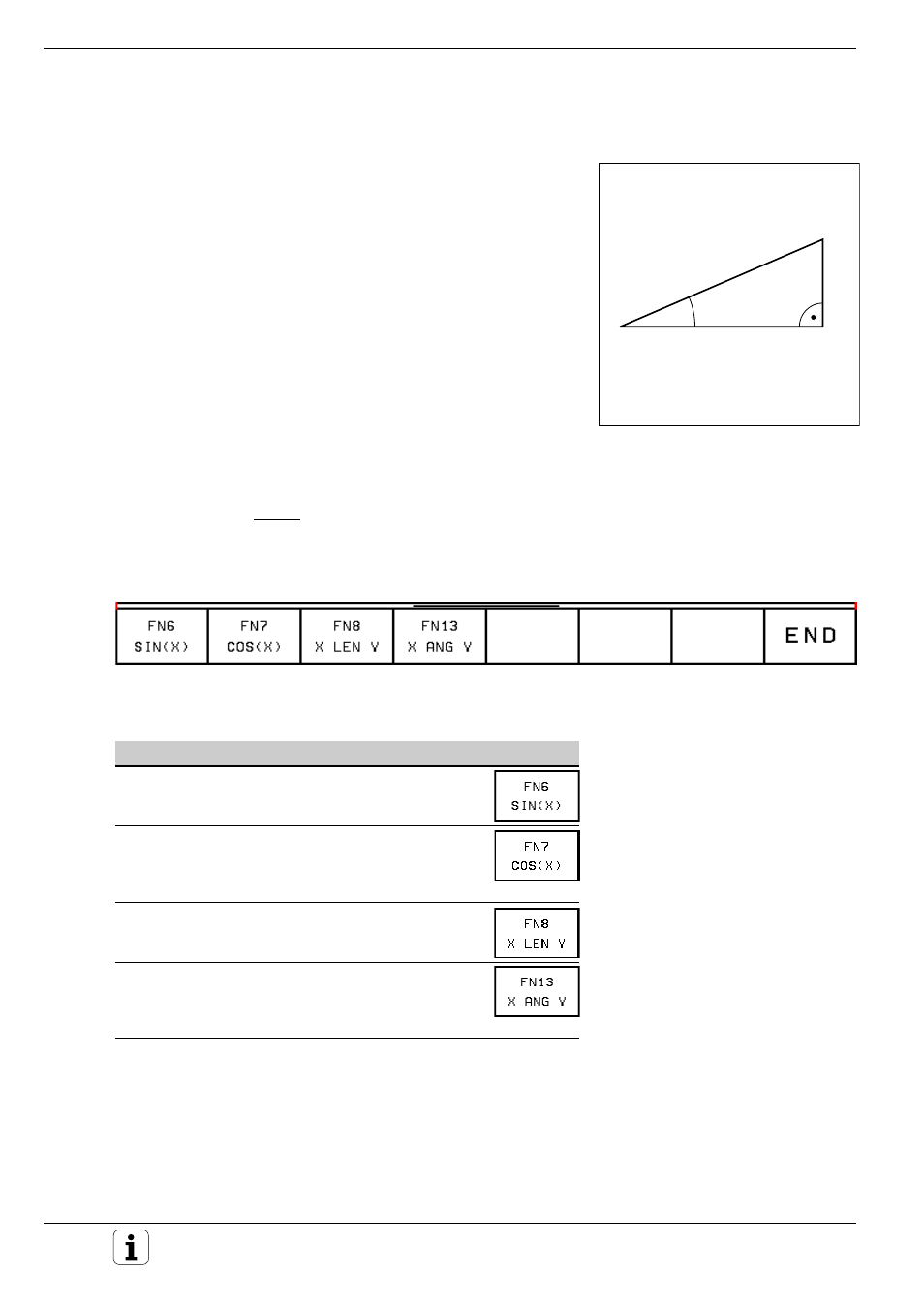
Abb. 7.3:
Seiten und Winkel am recht -
winkligen Dreieck
b
c
a
α
7.3 Winkelfunktionen (Trigonometrie)
Sinus, Cosinus und Tangens entsprechen den Seitenverhältnissen bei
einem rechtwinkligen Dreieck und erleichtern viele Berechnungen.
Bei einem rechtwinkligen Dreieck gilt:
Sinus:
sin
α
= a / c
Cosinus:
cos
α
= b / c
Tangens:
tan
α
= a / b = sin
α
/ cos
α
Dabei ist:
• c die Seite gegenüber dem rechten Winkel
• a die Seite gegenüber dem Winkel
α
• b die dritte Seite
Aus dem Tangens kann der Winkel wieder bestimmt werden:
α
= arctan
α
= arctan (a / b) = arctan (sin
α
/ cos
α
)
Beispiel:
a = 10 mm
b = 10 mm
α
= arctan (a / b) = arctan 1 = 45°
Weiterhin gilt:
a
2
+ b
2
= c
2
(a
2
= a
.
a)
c =
√
a
2
+ b
2
Nach anwählen der Winkelfunktionen steht folgende Softkey-Leiste zur
Verfügung:
Funktions-Übersicht
Softkey
FN6: SINUS
z.B. FN6: Q20 = SIN–Q5
Sinus eines Winkels in Grad (°) bestimmen und zuweisen
FN7: COSINUS
z.B. FN7: Q21 = COS–Q5
Cosinus eines Winkels in Grad (°) bestimmen
und zuweisen
FN8: WURZEL AUS QUADRATSUMME
z.B. FN8: Q10 = +5 LEN +4
Differenz aus zwei Werten bilden und zuweisen
FN13: WINKEL
z.B. FN13: Q20 = +10 ANG–Q1
Winkel mit arctan aus zwei Seiten oder sin und cos des
Winkels (0 - Winkel - 360°) bestimmen und zuweisen